Normal Equation: Intuition
Normal Equations is a method to solve for $\theta$ analytically.
The first step is to convert or represent the dataset in a Matrix and vector form.
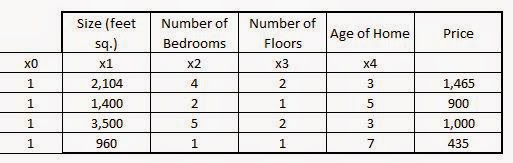
Consider the dataset:
The matrix X will be denoted as:
$X = \pmatrix{1 & 2104 & 4 & 2 & 3 \cr
1 & 1400 & 2 & 1 & 5 \cr
1 & 3500 & 5 & 2 & 3 \cr
1 & 960 & 1 & 1 & 7 \cr
}$
$m$ x $(n+1)$
The matrix Y will be denoted as
$Y = \pmatrix{1465 \cr 900 \cr 1000 \cr 435 \cr}$
m-dimensional vector
m training examples, (n+1) features
$\theta = (X^TX)^{-1}X^Ty$
When to use Normal Equation and when to use Gradient Descent:
The Gradient Descent algorithm needs an arbitary parameter $\alpha$ which is not needed in Normal Equations. Also, there is no need to do feature normalization in Normal Equation method. However, if the number of features are too large (n>10,000), Normal Equation method will be too slow because of difficulty in calculating the inverse of a very large matrix. Gradient Descent works well even if the number of features are in the order of ${10}^6$.
Normal Equations is a method to solve for $\theta$ analytically.
The first step is to convert or represent the dataset in a Matrix and vector form.
Consider the dataset:
The variables here are the predictors ($x_1,x_2,x_3,x_4$) and the outcome $y$. The coefficients will be $\theta_0,\theta_1, \theta_2, \theta_3 and \theta_4$.
The hypothesis:
$h_\theta(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\theta_4x_4+\theta_5x_5$
Another column needs to be added for $x_0$ which will just be filled with 1's to make the dataset look like:
The matrix X will be denoted as:
$X = \pmatrix{1 & 2104 & 4 & 2 & 3 \cr
1 & 1400 & 2 & 1 & 5 \cr
1 & 3500 & 5 & 2 & 3 \cr
1 & 960 & 1 & 1 & 7 \cr
}$
$m$ x $(n+1)$
The matrix Y will be denoted as
$Y = \pmatrix{1465 \cr 900 \cr 1000 \cr 435 \cr}$
m-dimensional vector
m training examples, (n+1) features
$\theta = (X^TX)^{-1}X^Ty$
When to use Normal Equation and when to use Gradient Descent:
The Gradient Descent algorithm needs an arbitary parameter $\alpha$ which is not needed in Normal Equations. Also, there is no need to do feature normalization in Normal Equation method. However, if the number of features are too large (n>10,000), Normal Equation method will be too slow because of difficulty in calculating the inverse of a very large matrix. Gradient Descent works well even if the number of features are in the order of ${10}^6$.

No comments:
Post a Comment